Metabolic reactions are represented as a stoichiometric matrix (S) of size m × n.

Every row of this matrix represents one unique compound (for a system with m compounds) and every column represents one reaction (n reactions).
The entries in each column are the stoichiometric coefficients of the metabolites participating in a reaction.
There is a negative coefficient for every metabolite consumed and a positive coefficient for every metabolite that is produced.
A stoichiometric coefficient of zero is used for every metabolite that does not participate in a particular reaction.
S is a sparse matrix because most biochemical reactions involve only a few different metabolites.

The flux through all of the reactions in a network is represented by the vector v, which has a length of n.
The concentrations of all metabolites are represented by the vector x, with length m.
The system of mass balance equations at steady state (dx/dt =0) is given:

Sv = 0

Any v that satisfies this equation is said to be in the null space of S.
In any realistic large-scale metabolic model, there are more reactions than there are compounds (n > m).
In other words, there are more unknown variables than equations, so there is no unique solution to this system of equations.

Although constraints define a range of solutions, it is still possible to identify and analyze single points within the solution space.
For example, we may be interested in identifying which point corresponds to the maximum growth rate or to maximum ATP production of an organism, given its particular set of constraints. FBA is one method for identifying such optimal points within a constrained space.

FBA seeks to maximize or minimize an objective function Z = c^Tv, which can be any linear combination of fluxes, where c is a vector of weights indicating how much each reaction (such as the biomass reaction when simulating maximum growth) contributes to the objective function.
In practice, when only one reaction is desired for maximization or minimization, c is a vector of zeros with a value of 1 at the position of the reaction of interest.

Optimization of such a system is accomplished by linear programming.
FBA can thus be defined as the use of linear programming to solve the equation Sv = 0, given a set of upper and lower bounds on v and a linear combination of fluxes as an objective function.
The output of FBA is a particular flux distribution, v, which maximizes or minimizes the objective function.

In summary the principle of Flux Balance Analysis will be as follows:

I) Derive mass balance equations from the reconstruction of a metabolic network and create the stoichiometric matrix (S).
II) Apply constraints of different types such as steady state, mass balance, thermodynamic (direction of a reaction, e.g. the flux vector (v) of a irreversible reaction is constrained to be greater than or equal to 0), and capacity (enzyme capacity or nutrient availability constrain the reaction flux to an upper bound (ub) and a lower bound (lb)) to limit the feasible solution space.
III) Find an optimal solution by the choice of a suitable optimization method (minimization or maximization of an objective function).

Here we provide some analysis derived from a constraint-based modeling:

Flux in two different situations:
It is possible to use FBA in order to compare changes in flux distributions between two different conditions. For examples, in the following pictures, the state of the E. coli core model with maximum growth rate as the objective under aerobic (a) and anaerobic (b) conditions has been demonstrated. The thick blue arrows represent reactions carrying flux, and the thin black arrows represent unused reactions. The metabolic pathways shown in these maps are glycolysis (Glyc), pentose phosphate pathway (PPP), TCA cycle (TCA), oxidative phosphorylation (OxP), anaplerotic reactions (Ana), and fermentation pathways (Ferm).

Robustness analysis:
It is also possible to explore response to flux changes of a given reaction for maximum growth rate (which is called robustness analysis).

Phenotypic phase planes:
Doing robustness analysis for two reactions is called Phenotypic Phase Planes. For example one could calculated growth with varying glucose and oxygen uptake rates and see if there are various regions based on such changes.

Gene knockout:
Another analysis would be deletion of each genes and explore what would be response of the system. Gene knockout screen will be possible for single and double deletion (gene knockout in pairs). For example one could delete each of the 136 genes in the core E. coli model and see the resulting relative growth rates. Some genes are always essential, and result in a growth rate of 0 when knocked out no matter which other gene is also knocked out. Other genes form synthetic lethal pairs, where knocking out only one of the genes has no effect on growth rate, but knocking both out is lethal.

Correlation:
Other useful analysis would be finding correlations between reactions. The correlation between the network reactions cancould be plotted for a set of reactions.

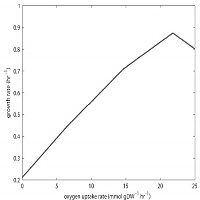
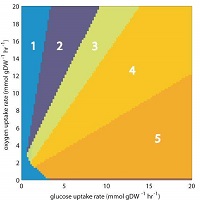
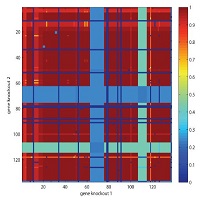
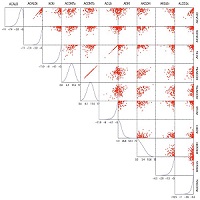
Robustness analysis	Phenotypic phase planes	Gene knockout	Correlation

... And there are even more analysis and concepts in the constraint-based modeling approach.
In the past decade, flux balance analysis (FBA) has been one of the most widely employed constraint-based techniques for systems-level analysis of living organisms. Remarkably, since 2000, there has been a steady increase in the number of FBA software (see for example "Software applications for flux balance analysis, Brief Bioinform. 2014, 15(1), 108-22")